【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。
本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.EM算法简介

我们经常会从样本观察数据中，找出样本的模型参数。最常用的方法就是极大化模型分布的对数似然函数。

但是在一些情况下，我们得到的观察数据有未观察到的隐含数据（学名是“隐变量”（latent variable）），此时我们未知的有隐含数据和模型参数，因而无法直接用极大化对数似然函数得到模型分布的参数。怎么办呢？这就是EM算法可以派上用场的地方了。

EM算法也称期望最大化（Expectation-Maximum，简称EM）算法。

EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一起来极大化对数似然，求解我们的模型参数（EM算法的M步)。由于我们之前的隐藏数据是猜测的，所以此时得到的模型参数一般还不是我们想要的结果。不过没关系，我们基于当前得到的模型参数，继续猜测隐含数据（EM算法的E步），然后继续极大化对数似然，求解我们的模型参数（EM算法的M步)。以此类推，不断的迭代下去，直到模型分布参数基本无变化，算法收敛，找到合适的模型参数。

从上面的描述可以看出，EM算法是迭代求解最大值的算法，同时算法在每一次迭代时分为两步，E步和M步。一轮轮迭代更新隐含数据和模型分布参数，直到收敛，即得到我们需要的模型参数。

对于 $m$ 个样本观察数据 $x = (x^{(1)},x^{(2)},…,x^{(m)})$ 中，找出样本的模型参数 $\theta$ ，极大化模型分布的对数似然函数如下：

$\theta = \arg \max \limits_{\theta} \sum^m_{i=1} \log P(x^{(i)};\theta)$

如果我们得到的观察数据有未观察到的隐含数据 $z=(z^{(1)},z^{(2)},…,z^{(m)})$ ，此时我们来最大化已观测数据的对数“边际似然”（marginal likelihood）：

$\theta = \arg \max \limits_{\theta} \sum^m_{i=1} \log P(x^{(i)};\theta) = \arg \max \limits_{\theta} \sum^m_{i=1} \log \sum_{z^{(i)}} P(x^{(i)},z^{(i)} ; \theta)$

公式的具体求解过程本文不再赘述。事实上，隐变量估计问题也可通过梯度下降等优化算法求解，但由于求和的项数将随着隐变量的数目以指数级上升，会给梯度计算带来麻烦；而EM算法则可看作一种非梯度优化方法。EM算法可看作用坐标下降法（见本文第2部分）来最大化对数似然下界的过程。

然后通过一个例子来形象化的理解EM算法。假设有两枚硬币A和B，它们随机抛掷的结果见下（H为正面，T为反面）：

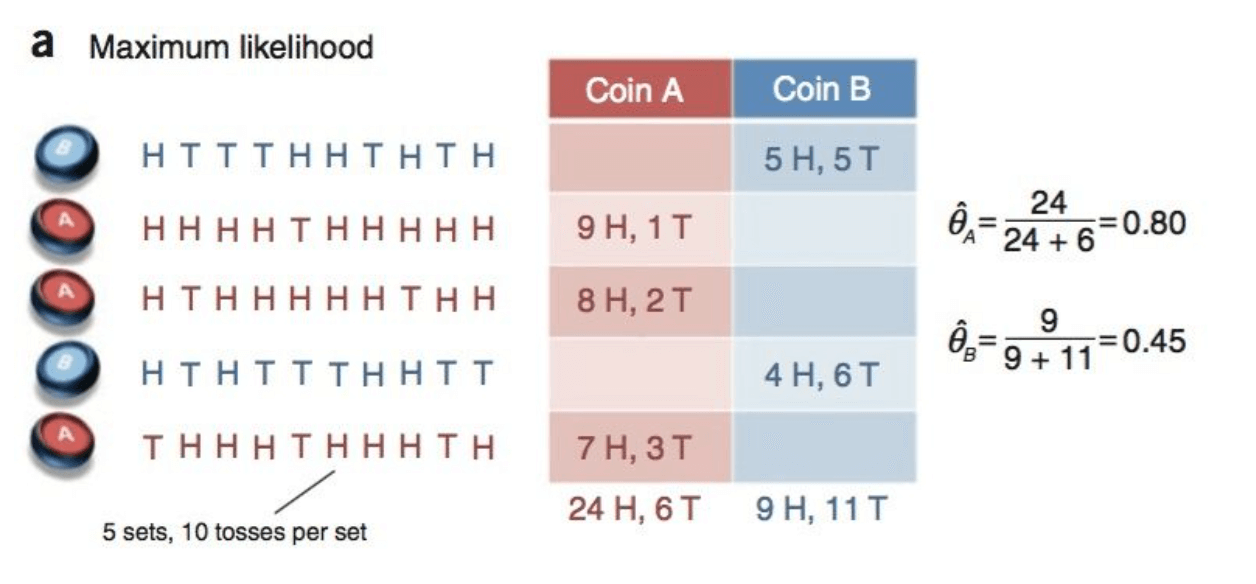
可以很容易估计出两枚硬币抛出正面的概率：

$\theta_A = \frac{24}{24+6}=0.80$

$\theta_B = \frac{9}{9+11}=0.45$

现在我们加入隐变量 $Z=(z_1,z_2,z_3,z_4,z_5)$ ，代表每一轮所用的硬币，即抹去每轮投掷的硬币标记：

这种情况下，我们该如何估计 $\theta_A$ 和 $\theta_B$ 的值？其解决方法就是先随机初始化 $\theta_A$ 和 $\theta_B$ ，然后用去估计 $Z$ ，然后基于 $Z$ 按照最大似然概率去估计新的 $\theta_A$ 和 $\theta_B$ ，循环至收敛。

假设随机初始化：

$\theta_A = 0.6$

$\theta_B = 0.5$

对于第一轮来说，如果使用硬币A，则得到5H5T的概率为 $C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5}$ ；如果使用硬币B，则得到5H5T的概率为 $C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}$ 。据此，我们便可以算出第一轮使用硬币A或硬币B的概率为：

$P_A = \frac{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5}}{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5} + C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}=0.45$

$P_B = \frac{C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5} + C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}=0.55$

剩余轮次，以此类推可得到：

以上就是E-Step。

接下来结合硬币A的概率和投掷结果，我们利用期望可以求出硬币A和硬币B的贡献。以第二轮硬币A为例：

$H : 0.80 * 9 =7.2$

$T : 0.80 * 1 = 0.8$

于是我们可以得到：

重新计算 $\theta_A$ 和 $\theta_B$ ：

$\theta_A = \frac{21.3}{21.3+8.6}=0.71$

$\theta_B = \frac{11.7}{11.7 + 8.4}=0.58$

这就是M-Step。然后如此反复迭代直至参数收敛。

2.坐标下降法

坐标下降法（coordinate descent）是一种非梯度优化方法，它在每步迭代中沿一个坐标方向进行搜索，通过循环使用不同的坐标方向来达到目标函数的局部最小值。

求解极大值问题时亦称“坐标上升法”（coordinate ascent）。

不妨假设目标是求解函数 $f(\mathbf x)$ 的极小值，其中 $\mathbf x = (x_1,x_2,…,x_d)^T \in \mathbb R^d$ 是一个 $d$ 维向量。从初始点 $\mathbf x^0$ 开始，坐标下降法通过迭代地构造序列 $\mathbf x^0,\mathbf x^1,\mathbf x^2,…$ 来求解该问题， $\mathbf x^{t+1}$ 的第 $i$ 个分量 $x^{t+1}_i$ 构造为：

$x^{t+1}_i = \arg \min \limits_{y \in \mathbb R} f(x^{t+1}_1,...,x^{t+1}_{i-1},y,x^{t}_{i+1},...,x^t_d)$

即固定其他因变量，只留一个因变量。此时求解 $f(x)$ 的最小值。这样问题就变得容易许多。

通过执行此操作，显然有：

$f(\mathbf x^0) \geqslant f(\mathbf x^1) \geqslant f(\mathbf x^2) \geqslant ...$

与梯度下降法类似，通过迭代执行该过程，序列 $\mathbf x^0,\mathbf x^1,\mathbf x^2,…$ 能收敛到所期望的局部极小点或驻点（stationary point）。

坐标下降法不需计算目标函数的梯度，在每步迭代中仅需求解一维搜索问题，对于某些复杂问题计算较为简便。但若目标函数不光滑，则坐标下降法有可能陷入非驻点（non-stationary point）。

【机器学习基础】第二十六课：EM算法

期望最大化（Expectation-Maximum，简称EM）算法，坐标下降法

1.EM算法简介

2.坐标下降法

3.参考资料

CATALOG

FEATURED TAGS