【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。
本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.连续值处理

到目前为止我们仅讨论了基于离散属性来生成决策树。本节我们来讨论在决策树学习中如何使用连续属性。

可将连续属性离散化，最简单的策略是二分法（C4.5决策树算法中采用的机制）。

给定样本集D和连续属性a，假定a在D上出现了n个不同的取值，将这些值从小到大进行排序，记为$\{a^1,a^2,…,a^n \}$。基于划分点t可将D分为子集$D_t^-$和$D_t^+$，其中$D_t^-$包含那些在属性a上取值不大于t的样本，而$D_t^+$则包含那些在属性a上取值大于t的样本。显然，对相邻的属性取值$a^i$与$a^{i+1}$来说，t在区间$[a^i,a^{i+1})$中取任意值所产生的划分结果相同。因此，对连续属性a，我们可考察包含n-1个元素的候选划分点集合：

即把区间$[a^i,a^{i+1})$的中位点$\frac{a^i+a^{i+1}}{2}$作为候选划分点。

将信息增益的公式加以改造：

举个例子，假设我们有如下西瓜数据集：

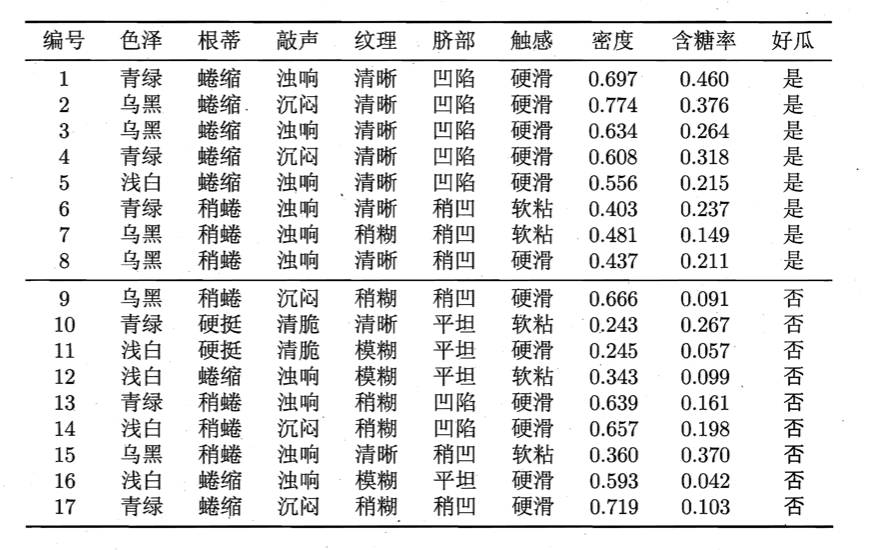
以连续属性“密度”为例，将17个属性值从小到大排列：0.243、0.245、0.343、0.360、0.403、0.437、0.481、0.556、0.593、0.608、0.634、0.639、0.657、0.666、0.697、0.719、0.774。根据式1.1，得到该属性的16个候选划分点：0.244、0.294、0.351、0.381、0.420、0.459、0.518、0.574、0.600、0.621、0.636、0.648、0.661、0.681、0.708、0.746。计算每个候选分割点的信息增益：

根据式1.2取信息增益的最大值0.262，对应于划分点0.381。同理，可得连续属性“含糖率”的信息增益为0.349，对应于划分点0.126。

⚠️与离散属性不同，若当前结点划分属性为连续属性，该属性还可作为其后代结点的划分属性。例如在父结点上使用了“密度$\leqslant$0.381”，不会禁止在子结点上使用“密度$\leqslant$0.294”。

2.缺失值处理

假设我们有含缺失值的西瓜数据集见下：

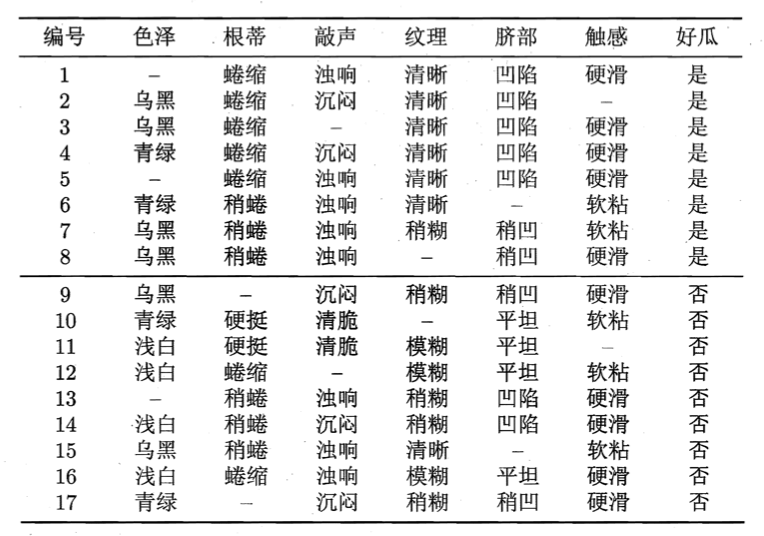
如果直接舍弃含有缺失值的数据，那么仅有4、7、14、16四个样本可用，显然是对数据信息极大的浪费。

我们需解决两个问题：

1. 如何在属性值缺失的情况下进行划分属性选择？
2. 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？

👉解决问题1：

给定训练集D和属性a，令$\tilde{D}$表示D中在属性a上没有缺失值的样本子集。我们可仅根据$\tilde{D}$来判断属性a的优劣。假定属性a有V个可取值$\{ a^1,a^2,…,a^V \}$，令$\tilde{D}^v$表示$\tilde{D}$中在属性a上取值为$a^v$的样本子集，$\tilde{D}_k$表示$\tilde{D}$中属于第k类$(k=1,2,…,\mid y \mid)$的样本子集，则显然有$\tilde{D}=\cup^{\mid y \mid}_{k=1} \tilde{D}_k$，$\tilde{D}=\cup^V_{v=1} \tilde{D}^v$。假定我们为每个样本x赋予一个权重$w_x$，并定义：

在决策树学习开始阶段，根结点中各样本的权重初始化为1。

直观地看，对属性a，$\rho$表示无缺失值样本所占的比例，$\tilde{p}_k$表示无缺失值样本中第k类所占的比例，$\tilde{r}_v$则表示无缺失值样本中在属性a上取值$a^v$的样本所占的比例。显然，$\sum^{\mid y \mid}_{k=1} \tilde{p}_k=1,\sum^V_{v=1} \tilde{r}_v=1$。

根据上述定义，将信息增益推广为：

其中，

👉解决问题2：

若样本x在划分属性a上的取值已知，则将x划入与其取值对应的子结点，且样本权值在子结点中保持为$w_x$。若样本x在划分属性a上的取值未知，则将x同时划入所有子结点，且样本权值在与属性值$a^v$对应的子结点中调整为$\tilde{r}_v \cdot w_x$。

C4.5算法使用了上述解决方案。

以上述含缺失值的西瓜数据集为例。该数据集一共包含17个样例，各样例的权值均为1。以属性“色泽”为例，有14个样例无缺失值，$\tilde{D}$的信息熵为：

令$\tilde{D}^1,\tilde{D}^2,\tilde{D}^3$分别表示在属性“色泽”上取值为“青绿”“乌黑”以及“浅白”的样本子集，有：

因此，样本子集$\tilde{D}$上属性“色泽”的信息增益为：

于是，样本集D上属性“色泽”的信息增益为：

同理可计算出所有属性在D上的信息增益：

• $Gain(D,色泽)=0.252$
• $Gain(D,根蒂)=0.171$
• $Gain(D,敲声)=0.145$
• $Gain(D,纹理)=0.424$
• $Gain(D,脐部)=0.289$
• $Gain(D,触感)=0.006$

因此，选择属性“纹理”对根结点进行划分。样例1,2,3,4,5,6,15进入“纹理=清晰”分支，样例7,9,13,14,17进入“纹理=稍糊”分支，样例11,12,16进入“纹理=模糊”分支，且样本在各子结点中的权重依旧保持为1。

⚠️样例8在属性“纹理”上出现了缺失值，因此它将同时进入三个分支，但权重在三个子结点中分别调整为$\frac{7}{15},\frac{5}{15},\frac{3}{15}$。

最终生成的决策树见下：

• Previous
  【深度学习基础】第二十六课：机器学习策略（上）
• Next
  【深度学习基础】第二十七课：机器学习策略（下）